Secretary Problem Variant Deep Dive
A deep dive into a variant of the secretary problem - no prereading required!
Introduction
The secretary problem (sometimes called the marriage problem) is a famous algorithmic puzzle with applications in social decision making. I’ve taken the initial problem setup from another great article
You are the HR manager of a company and need to hire the best secretary out of a given number N of candidates. You can interview them one by one, in random order. However, the decision of appointing or rejecting a particular applicant must be taken immediately after the interview. If nobody has been accepted before the end, the last candidate is chosen.
At this point, the following question is usually asked:
What strategy do you use to maximize the chances to hire the best applicant?
The well known solution to the problem (as \(N\) goes to infinity) is as follows:
- Reject the first \(\frac{N}{e}\) secretaries where \(e\) is Eulers number, and note down the best out of this group as \(\text{init}_{\max}\)
- Hire the first secretary after that point that is better than \(\text{init}_{\max}\)
While this may be an interesting question, it falls short of the real world scenario we are trying to model here in our opinion. If the secretaries are randomly distributed, the second best secretary out of the \(N\) should also be a pretty good hire, and same for the third best. In fact, a strategy that picks the best secretary 10 percent of the time and the worst secretary every other time should really be deemed worse than one that picks the best secretary 9 percent of the time and the second best the other 91 percent.
Our previous musings lead to the idea of trying to maximize the best secretary in expectation, where the best secretary of the group has the highest value of \(N\), the second best \(N - 1\), and so on until the worst secretary with a score of 1
Solution to the “Discrete Expected Secretary Problem”
Formal Setup/Ideas
Formally, we will consider a set of \(N\) secretaries with distinct scores from 1 to \(N\), and order them randomly. We will use the strategy of passing on some fixed number \(k\) secretaries then picking the next one better than all those we passed on, with \(k_{\text{opt}}\) being the optimal value for highest expected return.
If we can write the expected value in terms of \(k\), i.e.
\[\begin{equation} \label{eq:goal} \mathbb{E}[\text{Secretary chosen}] = f(k) \end{equation}\]then we can simply differentiate with respect to \(k\) and find the max by setting the derivative equal to zero. Let’s try that. From here on, \(k\) represents the number of secretaries we reject in part one of the algorithm.
Expectation Calculation
To tackle this problem, we will use the law of total expectation, and partition our possibilities based on the score of \(\text{init}_{\max}\), the best secretary from the initial rejected group. Notice that this value must be at least \(k\), since the initial group has \(k\) secretaries:
\[\begin{equation} \label{eq:total_prob} \mathbb{E}[\text{Secretary chosen}] = \sum_{i = k}^N \mathbb{P}[\text{init}_{\max} = i]\mathbb{E}[\text{Secretary chosen} | \text{init}_{\max} = i] \end{equation}\]From here, notice that calculating \(\mathbb{E}[\text{Secretary chosen} | \text{init}_{\max} = i]\) is relatively easy.
- If \(\text{init}_{\max} = N\), then the best secretary was in the rejecting group, and we are forced to choose the last secretary in the list of \(N\). The last secretary is distributed randomly between the worst and second best in this case (since the best is in the initial \(k\)), so the expected value is \(\frac{1 + (N - 1)}{2} = \frac{N}{2}\)
- If \(\text{init}_{\max} \neq N\), then the best secretary was not in the rejecting group, and any secretary better than \(\text{init}_{\max}\) has the same probability of being the first one to be found after all rejections. As a result, the expected value is the average of all of their scores, or \(\frac{(\text{init}_{\max} + 1) + N}{2}\)
These thoughts lead us to the new equation of:
\[\begin{equation} \label{eq:total_prob_simp} \mathbb{E}[\text{Secretary chosen}] = \mathbb{P}[\text{init}_{\max} = N]\frac{N}{2} + \sum_{i = k}^{N - 1} \mathbb{P}[\text{init}_{\max} = i]\frac{i + 1 + N}{2} \end{equation}\]We can again simplify, since the probability that \(\text{init}_{\max} = N\) (i.e. the best secretary of the first \(k\) is \(N\) ) is simply the probability that the best secretary (with score \(N\)) is in the first \(k\). Since everyone is randomly distributed, this occurs with probability \(\frac{k}{N}\):
\[\begin{equation} \label{eq:top_prob} \mathbb{P}[\text{init}_{\max} = N] = \mathbb{P}[\text{the top secretary is in the first $k$}] = \frac{k}{N} \end{equation}\]We now have:
\(\begin{equation} \mathbb{E}[\text{Secretary chosen}] = \frac{k}{N}\frac{N}{2} + \sum_{i = k}^{N - 1} \mathbb{P}[\text{init}_{\max} = i]\frac{i + 1 + N}{2} \end{equation}\) \(\begin{equation} \label{eq:total_prob_more_simp} \mathbb{E}[\text{Secretary chosen}] = \frac{k}{2} + \sum_{i = k}^{N - 1} \mathbb{P}[\text{init}_{\max} = i]\frac{i + 1 + N}{2} \end{equation}\)
What’s left is to determine \(\mathbb{P}[\text{init}_{\max} = i]\) in the other cases, and turn this whole thing into closed form. Here we will turn to combinatorics.
Since the secretaries are in a random order, all orderings have the same probability. As a result, we can find \(\mathbb{P}[\text{init}_{\max} = i]\) for any arbitrary \(i\) by counting how many orderings have \(i\) as the best secretary in the first \(k\) over the total number of secretaries.
Note that \(\text{init}_{\max} = i\) for some arbitrary \(i\) exactly when:
- The \(i\)th secretary is in the first \(k\)
- the \(k - 1\) other secretaries in the first \(k\) are worse than secretary \(i\).
Let’s count the number of valid orderings
\[\begin{equation} \underbrace{k}_{\text{put $i$ in the first $k$}}*\underbrace{\binom{i - 1}{k - 1}}_{\text{choose a group of $k - 1$ secretaries worse than $i$}}*\underbrace{(k - 1)!}_{\text{order secretaries worse than $i$}}*\underbrace{(N - k)!}_{\text{order rest}} \end{equation}\]The only difference between a valid ordering and an arbitrary ordering of the \(N\) secretaries is that for an arbitrary ordering, we can choose any subset to be in the first \(k\), and we can put element \(i\) anywhere:
\[\begin{equation} \underbrace{N}_{\text{put $i$ somewhere}}*\underbrace{\binom{N - 1}{k - 1}}_{\text{choose any $k - 1$ secretaries for the first $i - 1$ available spots}}*\underbrace{(k - 1)!}_{\text{order these $k - 1$ secretaries}}*\underbrace{(N - k)!}_{\text{order rest}} \end{equation}\]From here we can finally calculate the prbability as
\[\begin{equation} \mathbb{P}[\text{init}_{\max} = i] = \frac{\text{valid orderings}}{\text{total orderings}} = \frac{k \binom{i - 1}{k - 1}(k - 1)!(N - k)!}{N \binom{N - 1}{k - 1}(k - 1)!(N - k)!} = \frac{k}{N}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{equation}\]From here we can finally fully write the expected value of the secretary chosen from Equation (2) and (3) for an arbitrary stopping point \(k\) as
\[\begin{equation} \label{eq:first_exp_no_simplify} \frac{k}{2} + \sum_{i = k}^{N - 1}\frac{k}{N}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}}\frac{i + 1 + N}{2} \end{equation}\]Luckily, the result simplifies nicely into
\[\begin{equation} \label{eq:exp_simple} \frac{k}{2} + \frac{N - k}{2}\left(\frac{N + 1}{N} + \frac{k}{k + 1}\right) \\ \end{equation}\]Click here for the full proof (slightly involved)
Note that in every assignment, \(\text{init}_{\max}\) must be a value between \(k\) and \(N\). As a result, the sum of probabilities of \(\text{init}_{\max} = i\) for \(i\) between \(k\) and \(N\) must add to 1. We have that:
\[\begin{equation} \label{eq:identity_messy} 1 = \sum_{i = k}^N \mathbb{P}[\text{init}_{\max} = i] = \sum_{i = k}^N \frac{k}{N}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{equation}\]moving around some terms, we have that:
\(\begin{equation} \label{eq:identity} \frac{N - k}{k} = \sum_{i = k}^{N - 1}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{equation}\)
Click here for the full subproof of moving around terms
\[\label{subsec_init_proof_second} \begin{align*} & 1 = \sum_{i = k}^N \frac{k}{N}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \\ \implies & \frac{N}{k} = \sum_{i = k}^N\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \\ \implies & \frac{N}{k} = \sum_{i = k}^{N - 1}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} + 1 \\ \implies & \frac{N - k}{k} = \sum_{i = k}^{N - 1}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{align*}\]Via a similar process where we reject the first \(k + 1\) secretaries, we arrive at
\[\begin{equation} \label{eq:surprise_tool} \frac{N(N - k)}{k + 1} = \sum_{i = k}^{N - 1} i\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{equation}\]Click here for fully worked out similar process
Let’s consider rejecting the first \(k + 1\) secretaries, and finding the probability that secretary \(i + 1\) is the best secretary in this group. We can count the number of ways this happens in the same way as equation 9 to yield:
\[\begin{align*} \label{eq:combinatorics_app_1} & \mathbb{P}[\text{max out of $k +1$} = i + 1] \\ = & \frac{k + 1}{N}\frac{\binom{i}{k}}{\binom{N - 1}{k}} &&\text{same idea as Equation (9)} \\ = & \frac{k + 1}{N}\frac{\frac{i}{k}\binom{i - 1}{k - 1}}{\frac{N - k}{k}\binom{N - 1}{k - 1}} &&\text{comb. identities} \\ = & \frac{(k + 1)i}{N(N - k)}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} && \text{Equation (11)} \end{align*}\]Again, since the sum of these probabilities from \(i + 1 = k + 1\) to \(i + 1 = N\) covers all possible top rejecting people, we have that:
\[\begin{equation} \sum_{i = k}^{N - 1} \frac{(k + 1)i}{N(N - k)}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} = 1 \end{equation}\]This directly yields the result, or
\[\begin{equation} \frac{N(N - k)}{k + 1} = \sum_{i = k}^{N - 1} i\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}} \end{equation}\]Putting this all together, we get:
\[\begin{align*} & \mathbb{E}[\text{Secretary chosen}] \\ = & \frac{k}{2} + \sum_{i = k}^{N - 1}\frac{k}{N}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}}\frac{i + 1 + N}{2} && \text{Equation (10)}\\ = & \frac{k}{2} + \frac{k(N + 1)}{2N} \left(\sum_{i = k}^{N - 1}\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}}\right) + \frac{k}{2N}\left(\sum_{i = k}^{N - 1}i\frac{\binom{i - 1}{k - 1}}{\binom{N - 1}{k - 1}}\right) \\ = & \frac{k}{2} + \frac{k(N + 1)}{2N} \left(\frac{N - k}{k}\right) + \frac{k}{2N}\left(\frac{N(N - k)}{k + 1}\right) && \text{Equations (13) and (14)}\\ = & \frac{k}{2} + \frac{N - k}{2}\left(\frac{N + 1}{N} + \frac{k}{k + 1}\right) \end{align*}\]Using the chain/quotient rules, the derivative with respect to \(k\) works out to be
\[\begin{equation} \frac{\partial}{\partial k} \mathbb{E}[\text{Secretary chosen}] = \frac{1}{2} + \frac{-1}{2}\left(\frac{N + 1}{N} + \frac{k}{k + 1}\right) + \frac{N - k}{2}\frac{1}{(k + 1)^2} \end{equation}\]Finally, we can set this to zero to and solve for \(k\) to achieve a solution of
\[\begin{equation} k_{\text{opt}} = \sqrt{N} - 1 \end{equation}\]Click here for fully worked out maxima calculation
\[\begin{align*} & \frac{1}{2} + \frac{-1}{2}\left(\frac{N + 1}{N} + \frac{k}{k + 1}\right) + \frac{N - k}{2}\frac{1}{(k + 1)^2} = 0 \\ \implies & \frac{N(k + 1)^2 - (N + 1)(k + 1)^2 - Nk(k + 1) + (N - k)N}{2N(k + 1)^2} = 0 \\ \implies & N(k + 1)^2 - (N + 1)(k + 1)^2 - Nk(k + 1) + (N - k)N = 0 \\ \implies & -(N + 1)k^2 - 2(N + 1)k - (1 - N^2) = 0 \\ \implies & (N + 1)k^2 + 2(N + 1)k + (1 - N^2) = 0 \\ \implies & k = \frac{-2(N + 1) \pm \sqrt{4(N + 1)^2 - 4(N + 1)(1 - N^2)}}{2(N + 1)} \\ \implies & k = \frac{-2(N + 1) \pm 2(N + 1)\sqrt{1 - (1 - N)}}{2(N + 1)} \\ \implies & k = -1 \pm \sqrt{N} \end{align*}\]Success! we now know that we should only reject the first \(\sqrt{N} - 1\) secretaries, then pick the next one that is greater than all those we rejected. If this isn’t a whole number, we can simply pick the closest integer to \(\sqrt{N} - 1\)![]()
Visualizations/Intuition
In the original version of the problem, we had to reject the first \(\frac{N}{e}\), or \(~34\) percent of secretaries before beginning the next stage. This means that \(34\) percent of the time, the top secretary is in the rejection group and the algorithm fails! When optimizing for only the top secretary, we have to pick a random secretary with a relatively low expected score over 1/3 of the time.
This is more OK when the only goal is to try and maximize the probability of the highest secretary, but severely punishes our formulation where getting the second best secretary or third best is also a win.
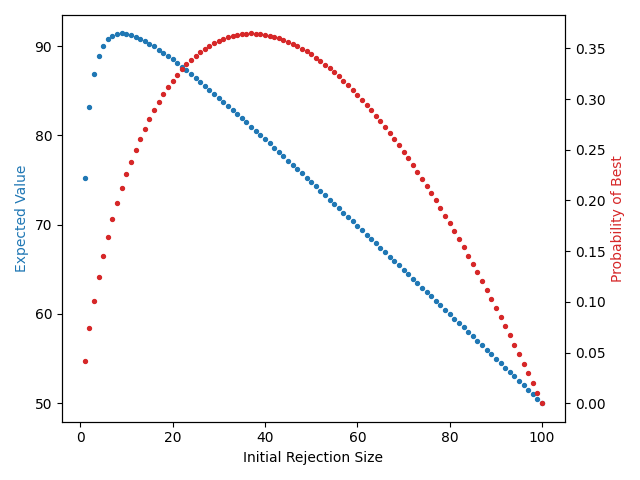
Here we visualize the expected value for picking the rejection number at 1 through 100 for \(N = 100\) as well as the probability of picking the best secretary. As predicted, the highest expected value is at \(k = \sqrt{100} - 1 = 9\), with an expected secretary score of 91.405, which is pretty good!! At this value, the probability of picking the best secretary is only 21 percent, as opposed to the 36 percent which occurs if we wait 36 people instead of 9. Since we only wait for the first 9 secretaries, our algorithm “fails” and is forced to pick the last secretary only \(9\) percent of the time.
A nicer formulation of the expected value is as follows:
\[\begin{equation} (n + 1)\left(1 - \frac{k}{2n} - \frac{1}{2(k + 1)}\right) \end{equation}\]Here, notice that if \(k\) is too big, the first negative term will reduce the epxected value, while if \(k\) is too small, the second negative term will reduce the expected value.